2023年8月总结
一呼一吸间的急促一呼一吸间的批判一呼一吸间的期待一呼一吸间的觉察一呼一吸间的自由一呼一吸间的喜悦 工作和成长018月重点研究了Prompt文本结构,一开始想找到一个万全的元结构落地到我们的视频脚本生成业务里,什么3R、RPPRWI、CRISPE、TRACI … 研究了很多案例和大语言模型之后发现,这些东西更适合叫做“功法”,是适合入门操作时不出错指南,它的粒度很粗同时宽容度很高。与任何大模型交流/调教的过程,基本就是一个拆解和明确任务的过程,为什么会有角色指定,就是要告诉它你是谁,如果你想告诉的更清晰,就是它应该掌握的技能明确地指定给它。这些 Structured Prompt 中无不贯穿着这些思想,指定工作流、指定受众、指定背景知识、指定目标…...
2023年7月总结
...
每个人都应该有点人生哲学(上)
01说到哲学好像是一个独立的大学术领域,其实关于人生哲学和每个人都息息相关,它就是一个个看上去有点宏大的问题,而每一个都应该主动去触达这些宏大的问题,正是这些问题构成我们独特的人生哲学。 不知道你怎么看待这些宏大的问题, 我活着有什么意义 我做的事情有什么意义 我此时此刻在追求什么 我是谁,什么构成了我 从我的观察来说,一部分人是完全拒绝或逃避这些问题,他们不去思考活着的意义 —— “问这种问题根本没意义好伐啦,钱不要赚的啊。”、“赶紧娶个老婆,好好工作赚钱,教育下一代要出息啊” 。显然,他们不会为这些宏大的问题苦恼,这些问题被他们归为了不需要思考的事情,我们接受了一种使命,并不加思索的执行着,也就是我们所说的 ——...
Github Copilot 实用上手指南
介绍 官网:https://github.com/features/copilot/ GitHub Copilot 是一款由 GitHub 和 OpenAI 合作开发的人工智能编程助手,可以根据编写的代码,自动生成可能的代码补全、函数调用、甚至是整个函数或代码块。它的定位是为开发者提供一个更加高效的编程工具,能够降低编程的难度和疲劳感,提高编程的质量和效率。 GitHub Copilot 的主要功能 代码补全:GitHub Copilot 可以基于当前代码的上下文,智能地生成代码片段和语句,提供代码自动补全的功能,从而减少编写代码的时间和错误。 函数调用:GitHub Copilot 可以根据当前上下文中已经存在的变量和方法,智能地推测出可能需要调用的函数,从而减少程序员的思考时间和错误率。 代码注释:GitHub Copilot 可以为代码自动生成注释,描述当前代码的功能和用途,从而帮助开发者更好地理解代码。 代码生成:GitHub Copilot...
Shader入门-07
前言最近项目太忙了,一个练习拼拼凑凑时间花了三天,不算满意,但总归完成了一版。加上这个练习在 _WorldSpaceLightPos0 获取不到上卡了一两个小时,整个人就有些烦躁,结果还是在放弃解决的时候发现是 untiy 设置的问题,有时候思路在一条路上走到黑了就逐渐疯狂 .. 花了很多时间在找图上,可视化的描述太重要了,但找来图也很难保持风格一致,总归看得不太舒服。 写完我从头看了下,前置的基础知识还包括线性代数基础,不然不好理解“点积”是做什么的,另外还有对于法向量的理解。 我把粗暴的结论写在这,当然这些基础概念我相信看文章的小伙伴不懂一定会动手搜索的 : ) 点积是两个向量的夹角余弦值乘以它们的长度之积,在这个练习中因为都做了归一化处理你可以当作就是 cosθ...
Shader入门-06
前言来上点难度 💪想不清楚就写写画画,没有什么比写下来更让人思路清晰了 效果圆角边框效果,支持改变边框的颜色、粗细、曲度 👉展示备份(国内节点)👇效果展示(科学上网) 代码123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263Shader "Unlit/AloeaShader06"{ Properties { _Radius ("BorderRadius", Range(0.01, 1)) = 0.1 _Border ("BorderWidth", Range(0, 1)) = 0.1 _Color ("BorderColor", Color) = (1,1,1,1) } SubShader ...
Shader入门-05
前言今天的练习知识部分比较简单 💪数字世界的颜色并不太好看,人的主观审美在数学表达里并不件容易的事 效果一个基础的血条,在进入低血量状态时闪烁报警👉展示备份(国内节点)👇效果展示(科学上网) 代码附件:贴图链接:https://pan.baidu.com/s/18R0Nd_KgD5R9qOJTLnrctg提取码:tvul 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263Shader "Unlit/AloeaShader05"{ Properties { _Health ("Health", Range(0, 1)) = 1 _MainTex ("Texture", 2D) = "white" {} } ...
Shader入门04
前言出去旅行了一周多,回来继续干活了 ✊云南的自然风光真是爽心悦目,坐到我小小的桌前倒有些不习惯了哈哈。 效果按照指定的混合程度图混合草地和岩石,地皮按照世界空间铺设 👉展示备份(国内节点)👇效果展示 (科学上网) 代码附件:贴图链接:https://pan.baidu.com/s/1_BS-VJculY-L3sKWgTtYAg提取码:6ue3 1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768Shader "Unlit/AloeaShader05"{ Properties { _MainTex ("Texture", 2D) = "white" {} // 材质1,草皮用 _Rock ("Texture", 2D)...
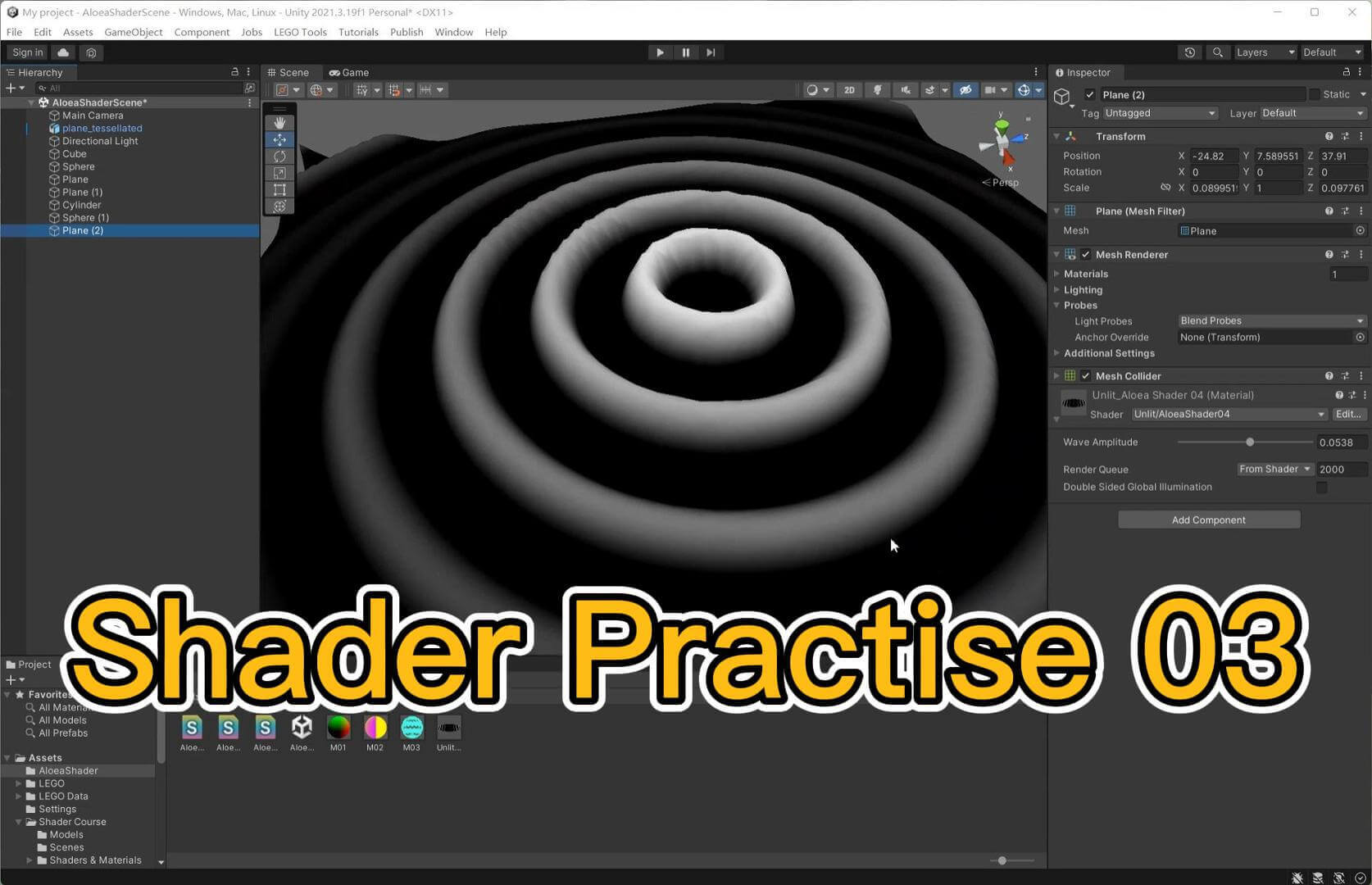
Shader入门-03
前言借由 Unity Shader 实战学习 Shader ! 带完整注释,一起学习 💪 效果从圆心慢慢荡漾开的水波,有高低起伏感 👉展示备份(国内节点)👇效果展示 (科学上网) 代码1234附件:1. 高面数平面链接:https://pan.baidu.com/s/1EObyLpQZDsQUXAxXS_QVtg 提取码:ij83 12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364Shader "Unlit/AloeaShader04"{ Properties { _WaveAmp ("Wave Amplitude", Range(0, 0.1)) = 0.05 } SubShader { Tags {...
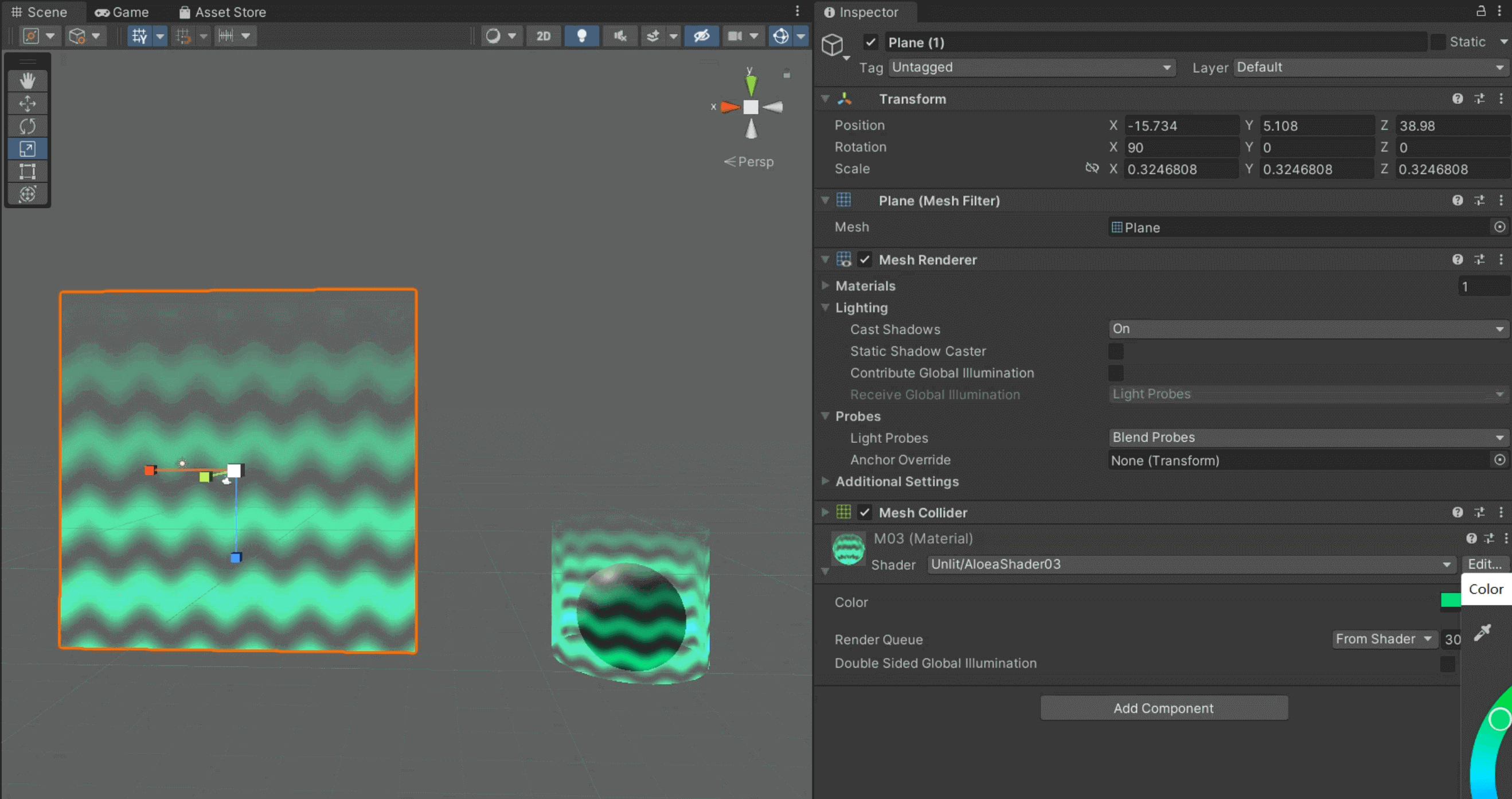
Shader入门-02
前言借由 Unity Shader 实战学习 Shader !带完整注释,一起学习 💪 效果环绕物体的水波纹特效,被神秘力量的光晕环绕,光晕从底部升起,向上逐渐消失 👉 展示备份(国内节点)👇 效果展示 (科学上网) 代码123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869Shader "Unlit/AloeaShader03"{ Properties { _Color ("Color", Color) = (0,0,0,0) // 参数声明 } SubShader { // 指定渲染顺序 Tags { ...