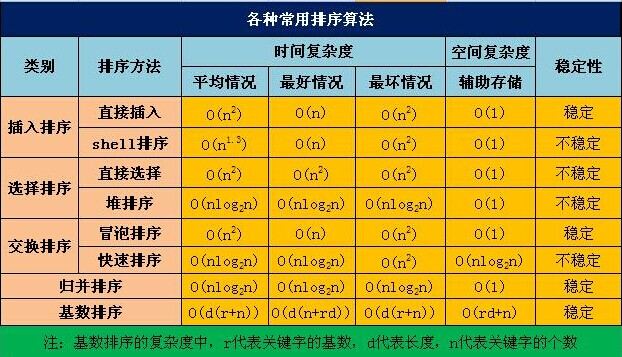
了解你使用的 Sort ( 实现剖析) - 1
先上图, 本篇文章涉及 插入排序 和 交换排序
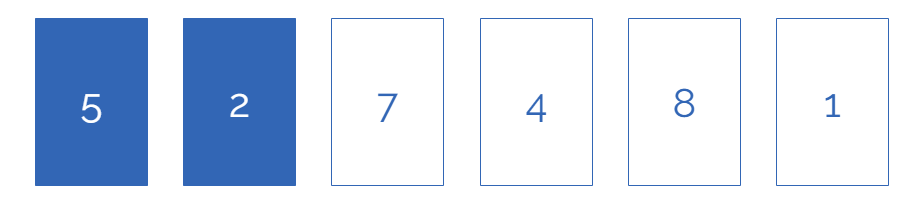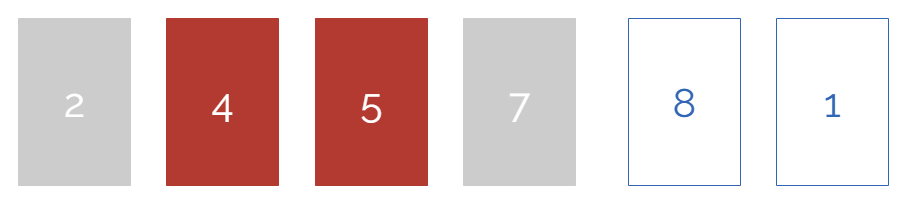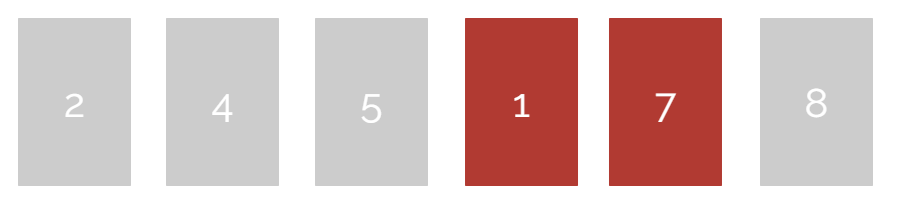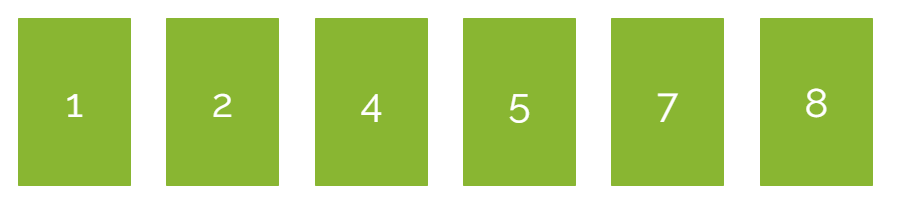
基础插入排序
思路:
- 将数组分为已完成排序部分和未完成排序部分,总是左侧为已完成部分
- 首先第 0 位归为已完成排序部分
- 将未完成排序部分中最左侧的数字依次与已完成排序部分的进行比较,如果左侧数字更大,则交换两那个数字,直至没有交换,至此已完成排序部分多一位
- 重复第三步操作直至未完成排序部分清空
参考动画去理解,小方块都绿是每个循环的结束 ↓
Shell 排序 (希尔排序)
由于基础插入排序每次都是一个挨着一个数字比较,希尔排序是对数字移动次数减少的一个改进算法。
- 定义一个正整数 d1 (可以理解为步数)
- 从第 0 位至 arr.length-d1 位遍历,将当前位 i 与 i+d1 为进行比较,如果第 i 位数大于 第 i+d1 位,则进行交换
- 再定义一个正整数 d2 (d2 < d1) 执行同2步骤
- 重复上述操作直至取 di=1,即对整个数组进行一次插入排序
可以理解为为了大概率减少数字间的交换,设计的一种增量逐步减少式的插入排序
一般 d1 选择 arr.length/2, d2=d1/2, d3=d2/2, 直至di=0
参考动画去理解, 小方块都绿是每个循环的结束 ↓ (d1=5, d2=2, d3=1)
冒泡排序
思路:
- 将数组分为已完成排序部分和未完成排序部分,总是右侧为已完成部分,初始全部在未完成部分
- 未完成排序部分从左至右依次比较相邻的两位,如果左侧大于右侧则交互交换,第一轮结束即已完成部分有一位
- 循环1步骤直全部完成
参考动画去理解, 小方块都绿是每个循环的结束 ↓

快速排序(快排)
快排使用分治法,加之跳跃式的交换通常在排序效率上相比其他算法更快
思路:
- 从数组中挑出一个数作为“基准”
- 重新排序数组,所有比基准小的放在基础前面,所有比基准大的方元素后面,相同的数可以任何一边,此时形成两个子集
- 在每个子集内执行2操作,这将会是递归的,直至子集为长度为1无法再执行操作
这个我觉得动画不是很直观,可以参考这篇分步小剧场
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.
Comment









