Test-Time-Training layers (TTT)
Test-Time-Training layers (TTT)
三句话介绍
TTT 层的优势是具有线性复杂度和表达性隐藏状态的序列建模层。
其在处理长文本和提高硬件效率方面非常有潜力。
关键思路是让隐藏状态改为机器学习模型,并将更新规则设为自监督学习的一步。
背景
Transformer 在长时间下表现良好,但具有二次复杂度
Transformer 有一个KV缓存,它会随着时间的推移不断增长。这个状态不会压缩任何历史上下文,但随着上下文长度的增加,成本也会越来越高。
对Transformer来说,每个token索引的平均复杂度在其32k上下文中不断减少。
RNN 层具有线性复杂度,但在长上下文中的性能受到隐藏状态的表达能力的限制
RNN 层必须将上下文压缩为固定大小的隐藏状态,作为一种压缩启发式,更新规则需要发现成千上万甚至数百万个token之间的底层结构和关系。
像 Mamba 这样的 RNN 层,会随着时间的推移压缩成一个固定大小的状态,它们虽然效率很高,但很难真正利用额外的条件信息。
TTT 的诞生
团队成员想:既然这样,为什么不把上下文压缩到模型的权重中——就像LLM处理互联网数据那样呢?
这种「隐藏状态模型」既能在时间上保持固定大小,又能大大增强表达能力。
价值
TTT 层直接替代了 Transformer 机制,解锁了具有表现力记忆的线性复杂度架构,使我们能够在上下文中训练包含数百万(未来可能是数十亿)个token的LLM。
核心点
提出了一种新的序列建模层,用机器学习模型取代RNN的隐藏状态,更新规则是自监督学习的一个步骤。
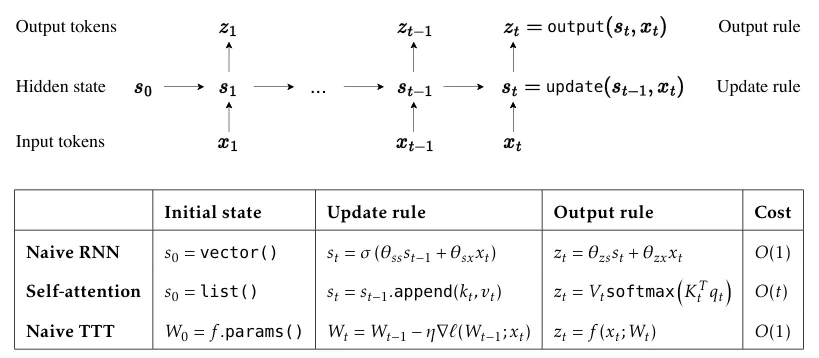
使用了自监督学习来更新隐藏状态的权重,对每个token进行一次梯度下降。在处理一个序列时,该状态已经在其上下文窗口中的token上「训练」过了。
值得注意的是,隐藏状态只存在于端到端架构中的一层。其他组件,比如QKV投影矩阵,是在预训练期间通过标准的交叉熵目标函数学习的。
因此,端到端架构实际上是在进行元学习,寻找压缩上下文的最佳方式,以便更好地预测下一个token,也就是在「学习如何在测试时学习」。
提出 TTT-Linear 和 TTT-MLP 两种实例,隐藏状态分别是线性模型和两层MLP。
TTT-Linear 和 TTT-MLP 在性能上与基线相当甚至更优。
与 Transformer 类似,TTT-Linear 能够通过考虑更多 token 来持续降低困惑度,而 Mamba 在处理超过 16k 上下文后就无法做到这一点。
TTT-MLP 则在内存I/O方面面临挑战,需要进一步研究。
通过 mini-batch TTT 和双重形式的创新,提高了在硬件上执行的效率,特别是在GPU和TPU上的优化。
为每个TTT mini-batch内的操作开发了一种对偶形式,以更好地利用现代GPU和TPU。这种对偶形式的输出与原始实现相当,但训练速度却快了5倍以上。
提出了未来研究的新方向,包括改进自监督任务的设计、系统优化、处理更长上下文和更大模型的能力,以及更大胆的f实现。
Source
https://arxiv.org/pdf/2407.04620
https://mp.weixin.qq.com/s/Z8BVt7g6rnuAFzoca1fjfg
https://mp.weixin.qq.com/s/khBJiXTk2NJIj-Cxnb8kAQ

