前言

最近项目太忙了，一个练习拼拼凑凑时间花了三天，不算满意，但总归完成了一版。加上这个练习在 _WorldSpaceLightPos0 获取不到上卡了一两个小时，整个人就有些烦躁，结果还是在放弃解决的时候发现是 untiy 设置的问题，有时候思路在一条路上走到黑了就逐渐疯狂 ..

花了很多时间在找图上，可视化的描述太重要了，但找来图也很难保持风格一致，总归看得不太舒服。


写完我从头看了下，前置的基础知识还包括线性代数基础，不然不好理解“点积”是做什么的，另外还有对于法向量的理解。

我把粗暴的结论写在这，当然这些基础概念我相信看文章的小伙伴不懂一定会动手搜索的 : )

  • 点积是两个向量的夹角余弦值乘以它们的长度之积，在这个练习中因为都做了归一化处理你可以当作就是 cosθ 。
  • 法向量是垂直于当前平面的单位向量。

效果

实现一版最基础的光照模型，包括环境光、表面漫反射、表面镜面反射。

👉展示备份（国内节点）
👇效果展示（科学上网）


代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
Shader "Unlit/AloeaShader07"
{
    Properties {
        _MainTex ("Texture", 2D) = "white" {}
        _Gloss ("Gloss", Range(1,100)) = 1
    }
  
    SubShader {
        Tags { "RenderType"="Opaque" "Queue"="Geometry" }
  
        Pass {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"
            #include "Lighting.cginc"
            #include "AutoLight.cginc"

            struct MeshData {
                float4 vertex : POSITION;
                float3 normal : NORMAL;
                float2 uv : TEXCOORD0;
            };

            struct Interpolators {
                float4 vertex : SV_POSITION;
                float2 uv : TEXCOORD0;
                float3 normal : TEXCOORD1;
                float3 worldPos : TEXCOORD2;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;
            float _Gloss;

            Interpolators vert (MeshData v) {
                Interpolators o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
                o.normal = UnityObjectToWorldNormal( v.normal );
                o.worldPos = mul( unity_ObjectToWorld, v.vertex ).xyz;
                return o;
            }

            float4 frag (Interpolators i) : SV_Target {

                // 环境光
                float ambient = unity_AmbientSky.w;
  
                // 漫反射
                float3 L = _WorldSpaceLightPos0.xyz;
                float3 N = normalize(i.normal);
                float3 diffuse = max(0, dot(L, N));

                // 镜面反射
                float3 V = normalize(_WorldSpaceCameraPos - i.worldPos);
                float3 H = normalize(L + V);
                float3 specular = max(0, dot(H, N));
                specular = pow(specular, _Gloss);
  
                return float4( (ambient + specular + diffuse) * _LightColor0.xyz * tex2D(_MainTex, i.uv) , 1);
            }
            ENDCG
        }
    }
}

效果调试

重要说明：
1. 请先看完下面知识点部分的【光照模型】
2. 本次练习的重点就是把光照模型的计算再写一遍


步骤一：
计算散射光 diffuse

1
2
3
4
5
6
7
8
9
10
11
float4 frag (Interpolators i) : SV_Target {
    // _WorldSpaceLightPos0 获取到场景内第一个平行光的单位矢量（方向）。
    // _WorldSpaceLightPos0 这个名字有点迷惑，由于平行光是无限远的，这里给的始终是单位向量，当作方向使用
    float3 L = _WorldSpaceLightPos0.xyz;
    // 世界空间下的法向量 （怎么转化的回顾下 [练习4]）。
    float3 N = normalize(i.normal);
    // 计算散射光：取入射光线 L 和 当前点的法向量 N 的点积，方向相反时会得到负数，需要处理范围至 [0, 1]。
    float3 diffuse = max(0, dot(L, N));

    return float4(diffuse, 1);
}

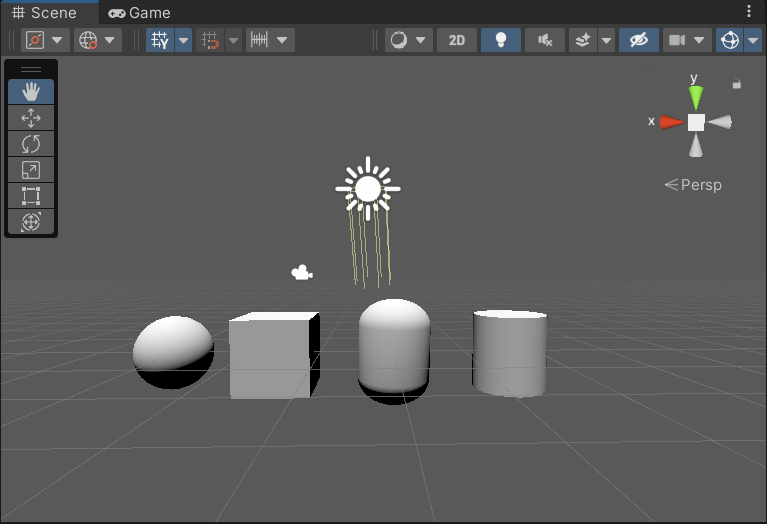
步骤二：
计算镜面反射光 specular

1
2
3
4
5
6
7
8
9
10
11
12
13
 float4 frag (Interpolators i) : SV_Target {
    // 世界空间下的法向量
    float3 N = normalize(i.normal);
    // 计算相机方向向量
    // _WorldSpaceCameraPos 是相机在世界空间下的位置，worldPos 是当前顶点在世界空间下的位置
    float3 V = normalize(_WorldSpaceCameraPos - i.worldPos);
    // 计算 blinn phone 模型中的中间向量 H
    float3 H = normalize(L + V);
    // 计算反射光：取 中间向量 H 和 顶点法向量 N 的点积，限制数值范围在 [0,1]
    float3 specular = max(0, dot(H, N));

    return float4(specular, 1);
}

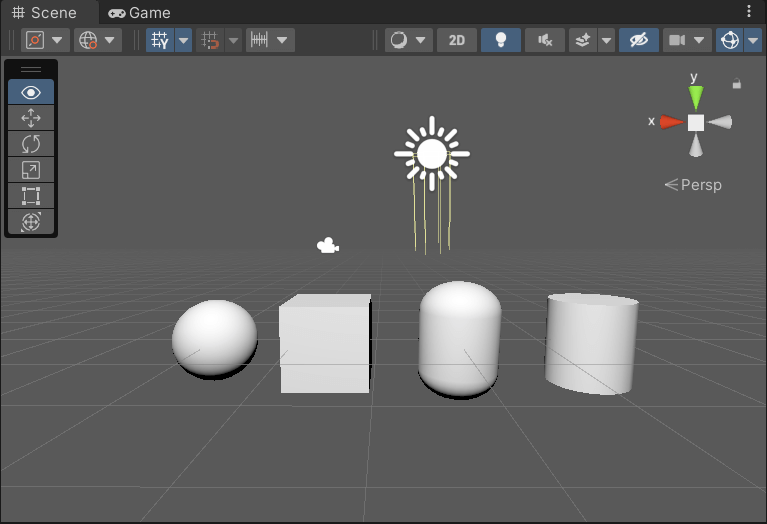
步骤三：
接入光泽度 _Gloss，测试反射光的面积和亮度

1
2
3
4
5
6
7
8
9
10
 float4 frag (Interpolators i) : SV_Target {
    float3 N = normalize(i.normal);
    float3 V = normalize(_WorldSpaceCameraPos - i.worldPos);
    float3 H = normalize(L + V);
    float3 specular = max(0, dot(H, N));
    // 接入参数 _Gloss
    specular = pow(specular, _Gloss);
    
    return float4(specular, 1);
}

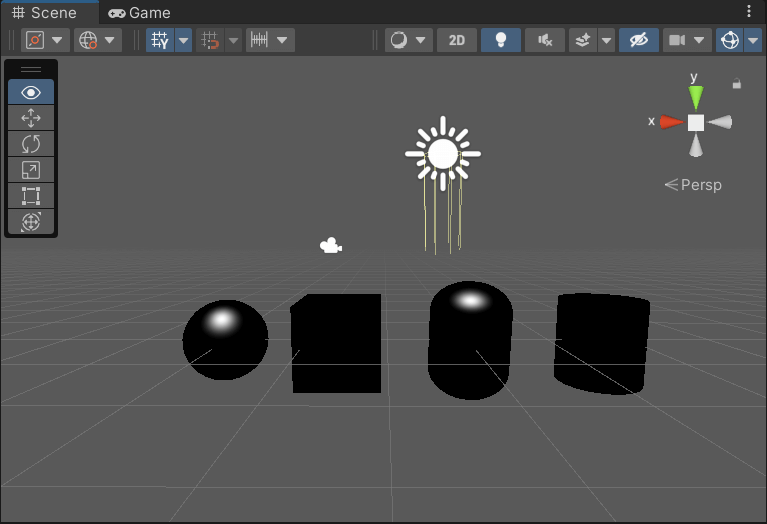
步骤四：
最后接入环境光、材质的纹理、光照的颜色

1
2
3
4
5
6
7
8
9
10
11
 float4 frag (Interpolators i) : SV_Target {
    float ambient = unity_AmbientSky.w;
    float3 N = normalize(i.normal);
    float3 V = normalize(_WorldSpaceCameraPos - i.worldPos);
    float3 H = normalize(L + V);
    float3 specular = max(0, dot(H, N));
    specular = pow(specular, _Gloss);
    // 表面的光照强度等于 ambient + specular + diffuse
    // 接入光照颜色 _LightColor0.xyz、材质纹理 tex2D(_MainTex, i.uv)
    return float4( (ambient + specular + diffuse) * _LightColor0.xyz * tex2D(_MainTex, i.uv) , 1);
}

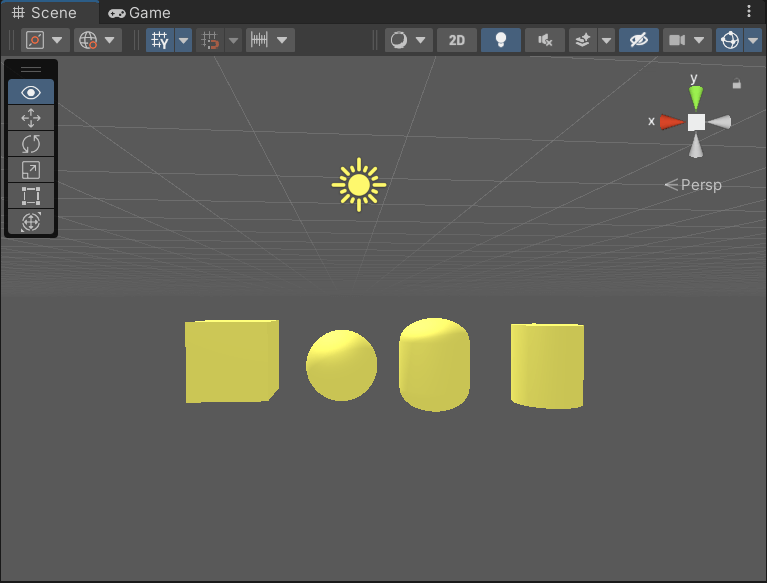
知识点

光照模型 - Lambert


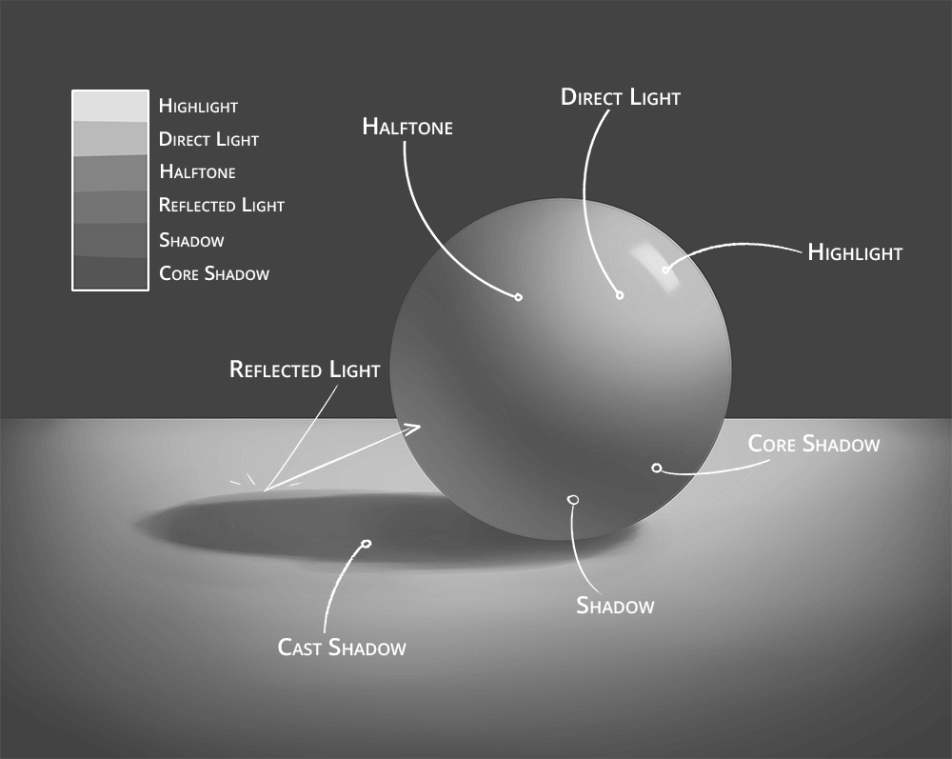
先借由这张图回顾下物理世界中一个物体对于光是如何反应的。

在任何一个环境场内，假设有一束无限远的方向光，那么首先在球体朝向光的那一半面积是会被照亮的，而另一半是不会被这束光直接照亮的。

同时，取决于我们的观测位置、球体表面的光泽度、方向光的强度，我们会看到表面尤其高亮的一块光斑。

与此同时，方向光在环境中其他物体/墙壁上反射出的光线也会照亮球体，让一部分在背光处的面被照亮。




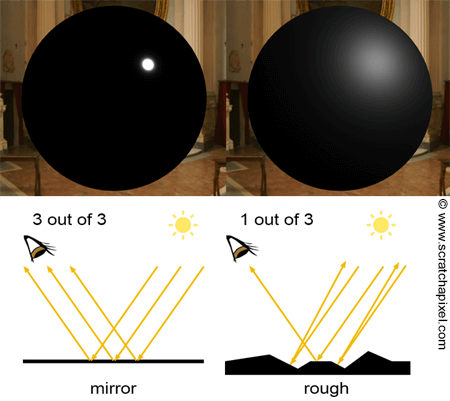
我们首先来进入一下漫反射的部分，也就是经典的 Lambert 光照模型。

已知物理世界是没有绝对光滑的表面的，任何表面由于凹凸不平会出现各个方向的反射，而 Lambert 光照假设表面对所有入射光线具有相同的反射率，那么表面每个点上漫反射的光照强度只取决于入射光的角度和法线的夹角。

其公式为 DiffuseLight = Kd * I * max( dot(N,L) )

其中 dot(N,L) 得到法线和入射光夹角的余弦，I 是入射光的强度即 Intensity，Kd 为表面的漫反射系数。


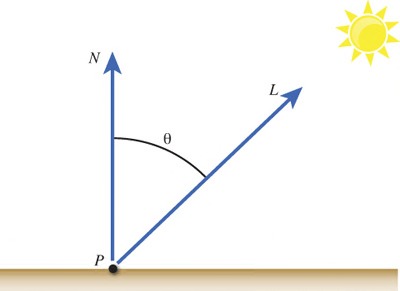
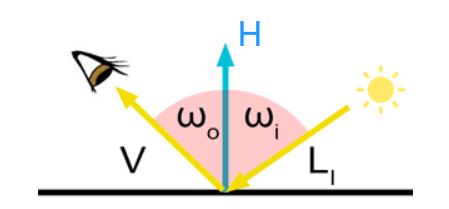
光照模型 — Phong Lighting

最基础的光照模型 Phong Lighting 将物体表面的反射光分为漫反射光和镜面反射两个部分，其中漫反射我们在上面的 Lambert Lighting 中已经了解过，而镜面反射，也就是视觉效果上的高亮效果，取决于入射光线反射后与视线方向的角度。

参考下图，入射光线 L 对应当前表面法向量 N 上反射出光线 R，当视线 V 的方向和 R 重叠时，高亮是最为强的，当 V 和 R 的夹角越大，观察到的镜面反射的效果则越弱。


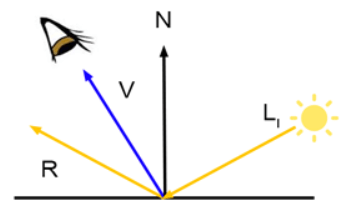
其实这个模型非常的简单，所有公式也很干净。

其公式为 max(0, dot(V,R))

其中 V 是视线向量，R 是光线反射向量。


光照模型 — Blinn Phong Lighting

整体上和 Phone Lighting 是接近的，差别是 Blinn-Phone 模型在镜面反射光照的计算中不依赖反射光线向量 R 了，而是使用一个所谓的中间向量 H。

其公式为 pow(max(0, dot(L, H)), Gloss)

其中 H 等于 (L + V)/(|| L + V ||) 也就是入射光线 L 和视线方向 V 的中间单位向量。


从效率上来讲，当视线和光线都距离表面无限远的时候，H 这个中间向量几乎就是常量，而 Phone 模型下则仍需要计算每一个点的反射光线。

从效果上来说，在 Phone Lighting 的方式中，对于一个平面来说镜面反射总是圆形的，而采用 Blinn Phong Lighting 后从一些角度看则是椭圆形的，像在太阳靠近地平面这样的场景下就要更真实。


Phone Light 的反射高亮

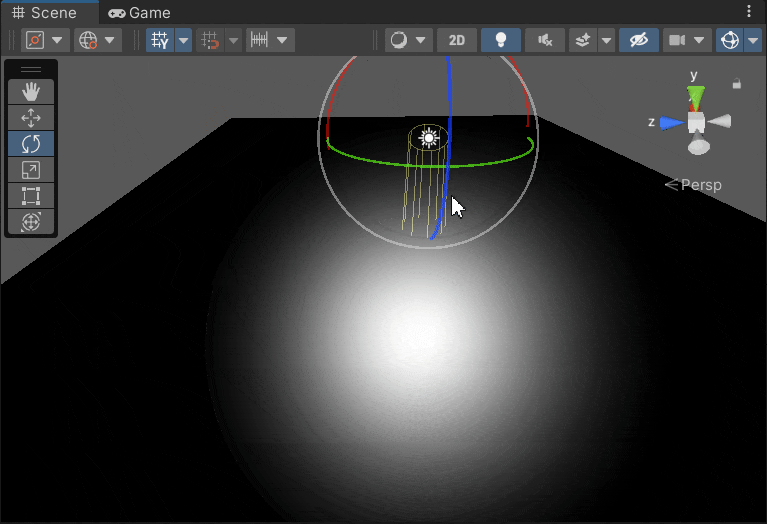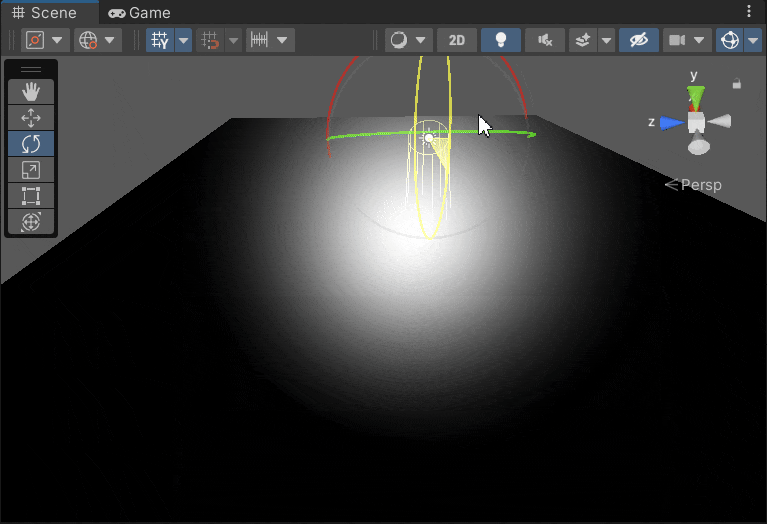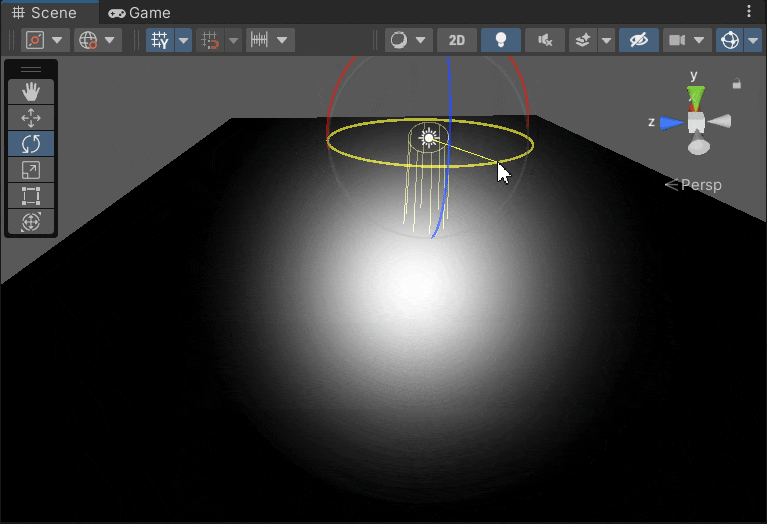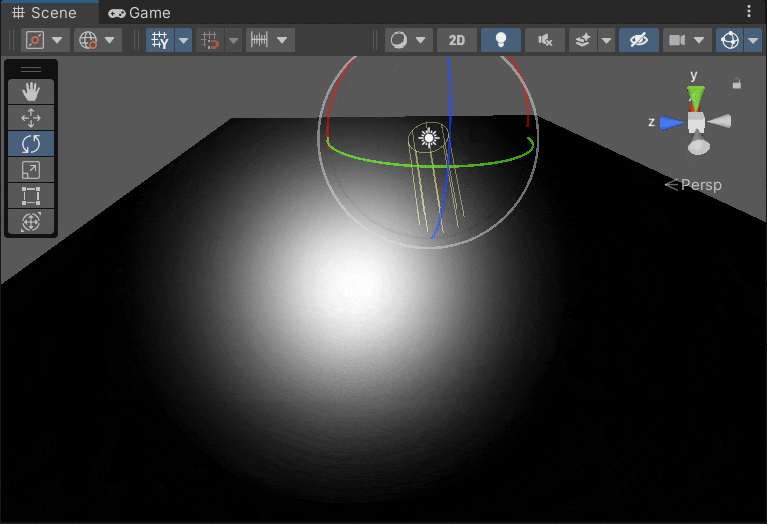
Blinn Phone Light 的反射高亮


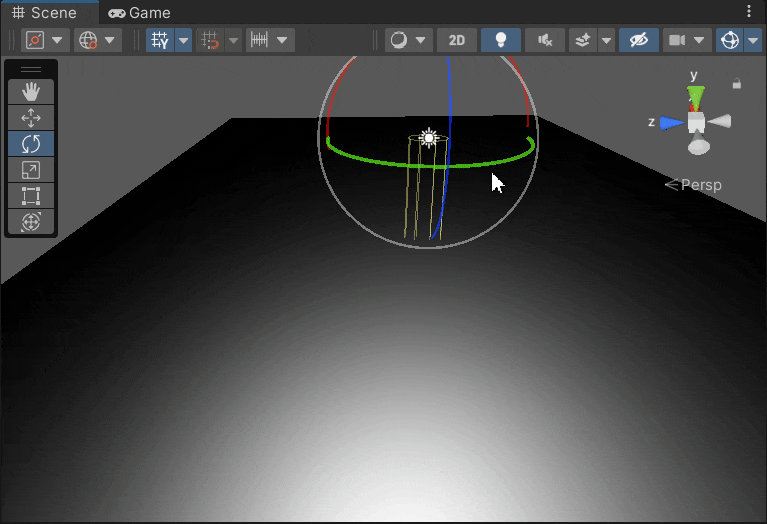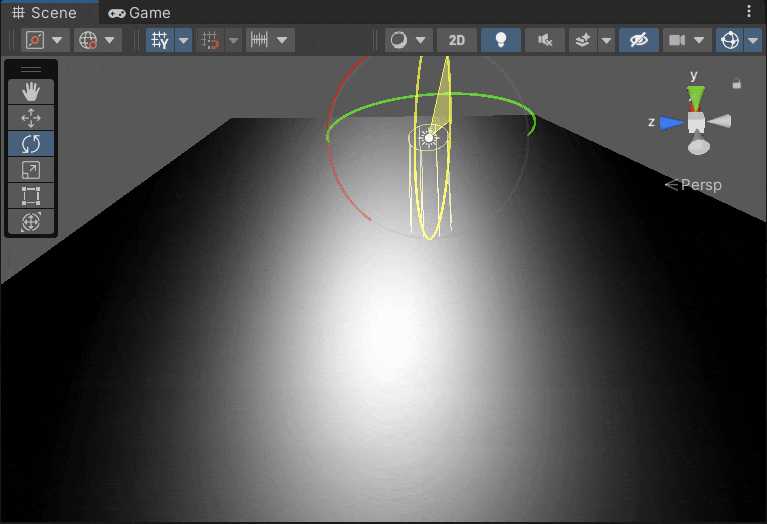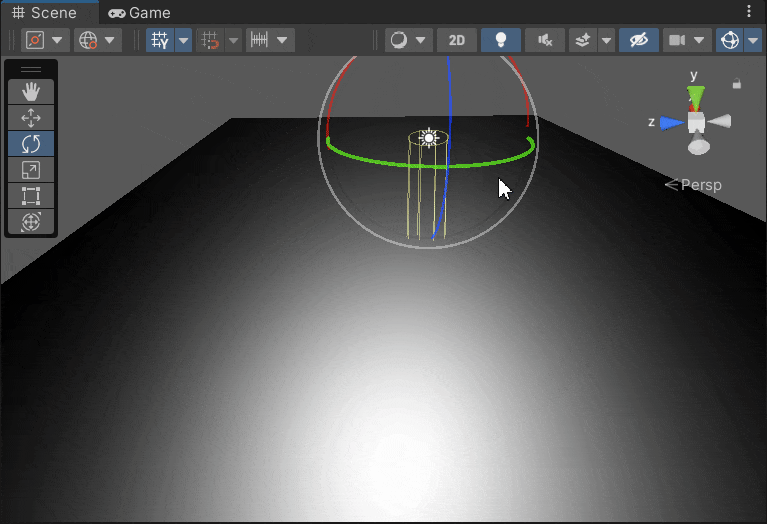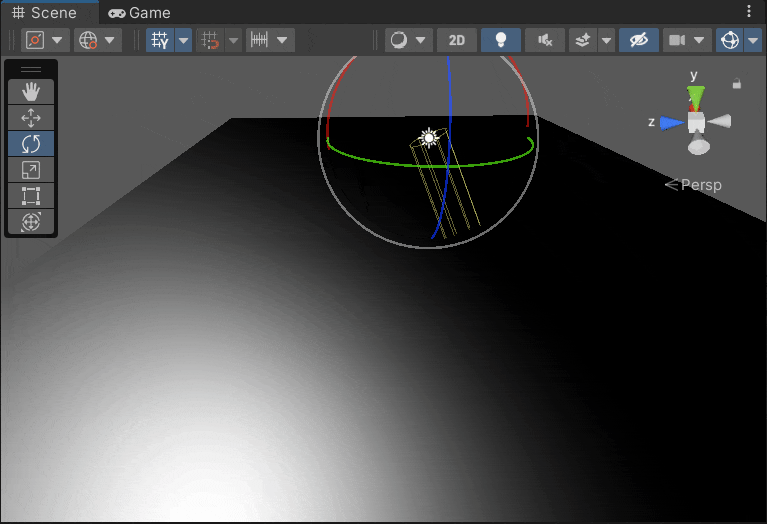
总结

今天的练习中主要涉及了环境光+漫反射光+镜面反射光组合的基础光照模型。

在光照模型领域，还有其他很有意思的光照计算方式。比如说变体的 Half-Lambert , 在表面较暗的区域带来更多光照，整体散射过渡更加光滑一些；还有 Banded-Lighting 让光照像波段一样阶梯型变化；Minnaert Lighting 模型特别适合用于凹凸不平的表面，那些有大量反向散射的表面，比如月亮、地毯；还有像 Oren-Nayer Lighting 这种基于半角向量的漫反射模型，来模拟更粗糙表面的效果…

看来，很适合把这批都练手一下呢 : ）

最后的最后，还是需要再次说明一下，图形学的光照模型都是一种数学上的近似模拟，而不是真实世界的表达。 —— 你怎么放飞想象都可以，但不要指着真太阳说它渲染得真细腻。