Number.EPSILON
今天介绍一个新的属性 - Number.EPSILON 用来表示 JS 中计算时的误差范围。
这个属性是 ECMAScript 2015 (6th Edition, ECMA-262) 开始支持的,兼容性上 IE 至今未支持..
EPSILON属性的值接近于 2^-52,表示1与大于1的最小浮动数之前的差值。 可以这么理解,它表示JS下进行计算时的最小精度,如果误差小于这个值可以认为没有意义。
利用 Numer.EPSILON 可以解决精度计算误差的问题,比如经典的 0.1 + 0.2 != 0.3
1 | x = 0.2; |
EPSILON(ε0)在数学中是序数,表示最小的数字
Q1. 精度运算问题中,为什么 0.1+0.2 != 0.3, 0.2 + 0.2 == 0.4 ?

这就涉及到计算机组成原理中关于数据存储的问题了,0.1+0.2 的计算步骤为
1 | // 0.1 和 0.2 都转化成二进制后再进行运算 (尾数部分52位,表达不了的会进行舍弃-精度丢失) |
同理你可以算出 0.2+0.2 = 0.0110011001100110011001100110011001100110011001100110100 // 转成十进制刚好0.4
所以我们并不会常遇到这个问题
Q2. JS的数字表达中精度为16位,那么为什么0.1+0.2=0.30000000000000004,这不是17位了吗
这是一个容易混淆的点,在JS的数字表达中确实默认精度为16位,但计算中不会进行舍弃
1 | var a = 0.3 // 0.3 |
Q3. 数字精度位数怎么得出的
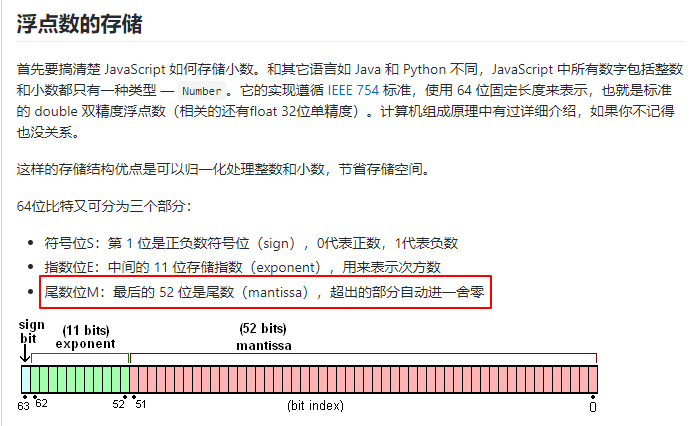
首先需要了解浮点数的存储,如上图,更详细可以看这篇文章
因为尾数位有52位,能表达的最大数 9.007199254740992 ,数一下得出16位。
Other
写文章中发现一个网站,免费在线虚拟机,搭配 jsfiddle 可以实现在线测各种系统和浏览器的兼容性问题 ~
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Luhui's Personal Website!
评论


